딥러닝에서 손실함수(loss function)란?

딥러닝에서 손실 함수(loss function)는 모델의 출력과 실제값 사이의 오차를 측정하는 함수입니다. 모델이 예측한 값과 실제 값이 일치하면 손실 함수의 값은 작아지며, 이 오차를 최소화하는 것이 딥러닝의 목표 중 하나입니다. 손실 함수는 모델이 학습하는 동안 사용되며, 모델의 가중치(weight)를 업데이트하는 데 사용됩니다.
딥러닝에서 사용되는 대표적인 손실 함수에는 다음과 같은 것들이 있습니다.
Mean Squared Error(MSE)
MSE는 예측값과 실제값 사이의 평균 제곱 오차를 계산합니다. 실제값과 예측값의 차이를 제곱하여 평균을 구한 값입니다.
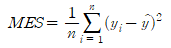
여기서, y는 실제값, y^는 예측값, n은 샘플의 개수입니다. MSE는 회귀(Regression) 문제에서 주로 사용됩니다.
import numpy as np
def mse(y_true, y_pred):
return np.mean(np.square(y_true - y_pred))
Binary Cross-Entropy Loss
이진 분류(Binary Classification) 문제에서 사용되는 손실 함수입니다. 예측값이 0 또는 1일 때, 실제값과 예측값의 차이를 계산합니다.

여기서, y는 실제값, y^는 예측값, n은 샘플의 개수입니다. 이 손실 함수는 분류 문제에서 주로 사용됩니다.
import numpy as np
def binary_crossentropy(y_true, y_pred):
return -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))Categorical Cross-Entropy Loss
다중 분류(Multi-class Classification) 문제에서 사용되는 손실 함수입니다. 클래스의 개수만큼의 차원을 갖는 확률 분포에서 실제 클래스와 예측 클래스 사이의 차이를 계산합니다.
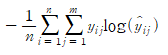
여기서, y는 실제값, y^는 예측값, n은 샘플의 개수, m은 클래스의 개수입니다. 이 손실 함수는 다중 분류 문제에서 주로 사용됩니다.
import numpy as np
def categorical_crossentropy(y_true, y_pred):
return -np.mean(np.sum(y_true * np.log(y_pred), axis=-1))Hinge Loss
SVM(Support Vector Machine)에서 사용되는 손실 함수입니다. SVM은 선형 분류 모델로서 Hinge Loss는 실제값과 예측값 사이의 차이가 일정 이상인 경우에만 오차를 계산합니다. 차이가 작으면 오차를 계산하지 않으므로 모델이 조금씩 틀리는 경우에는 학습이 더 원활해지게 됩니다.
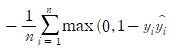
import numpy as np
def hinge(y_true, y_pred):
return np.mean(np.maximum(0., 1. - y_true * y_pred))Kullback-Leibler Divergence(KLD)
확률 분포 간의 차이를 계산하는 손실 함수입니다. 실제 분포와 예측 분포 사이의 차이를 측정합니다.

여기서, y는 실제 분포, y^는 예측 분포, n은 클래스의 개수입니다. 이 손실 함수는 분류 문제에서 주로 사용됩니다.
import numpy as np
def kld(y_true, y_pred):
return -np.mean(np.sum(y_true * np.log(y_pred / y_true), axis=-1))Dice Loss
세그멘테이션(Segmentation) 문제에서 사용되는 손실 함수입니다. 예측 값과 실제 값 사이의 Dice 계수를 이용하여 오차를 계산합니다. Dice 계수는 두 집합 사이의 유사성을 측정하는 지표입니다.

여기서, y는 실제값, y^는 예측값, n은 샘플의 개수입니다.
딥러닝에서 사용되는 손실 함수는 다양하지만, 주로 사용되는 손실 함수는 회귀 문제에서는 MSE, 분류 문제에서는 Cross-Entropy Loss입니다. 그러나 문제의 특성에 따라 다른 손실 함수를 사용할 수도 있습니다.
import numpy as np
def dice_loss(y_true, y_pred, smooth=1):
intersection = np.sum(y_true * y_pred)
union = np.sum(y_true) + np.sum(y_pred)
dice = (2. * intersection + smooth) / (union + smooth)
return 1. - dice'Study > Deep Learning' 카테고리의 다른 글
| 베이지안 딥러닝 (0) | 2023.04.03 |
|---|---|
| 딥러닝에서 최적화 알고리즘이란? (0) | 2023.03.31 |
| 딥러닝에서 데이터 분포란? (0) | 2023.03.30 |
| 딥러닝에서 확률과 통계 (0) | 2023.03.30 |
| 데이터 전처리 기술 [python] (0) | 2023.03.27 |








